pouët.net

I found a way to rasterize an octree in an isometric perspective, wrote a blog on gamedev, maybe someone is interested.
https://www.gamedev.net/blogs/entry/2268591-rasterize-voxels/

Interested surely. But you maybe forgot to mention that your algorithm is written in your own esoteric programming language...

Can you give a short comprehensive description of what your algorithm does in contrast to other typical implementations?

Sure

The main idea is, an octree in isometric is self similar, then, a double array (X Y) for children cover for a pixel, can be used for traverse the octree with change of scale, is like ray tracing, but the intersection with cubes are the AND operator.

I personally think that forth is not an esoteric language, rather it is an unknown and underrated language

all the post are in https://www.gamedev.net/blogs/blog/4192-experimental-graphics-technology/

I feel like being asked to read a tech manual in esperanto.

(meaning, I'm not going to learn a language just to understand the meaning of the text). Perhaps try something more well-known like a C derivate or JavaScript next time, perhaps you'll have a bigger audience.

Does the program written in your custom Forth-like language iterate over pixels like a pixel shader (hence something more like raytracing), or does it iterate through the voxels and then splat / plot each voxel once?

I think I get how the AND operation on the "X" and "Y" bit arrays performs an intersection between pixel-space rectangles (which are the bounding rectangles in screenspace of the nodes in the octree). What I don't yet understand is how this is any more efficient than depth-sorting the voxels (with the aid of the octree) and splatting / plotting them one after another.

If you can write some pseudo-code of your algorithm I think it would help us non-Forth-coders to understand your idea.

first question, like pixel shader... iterate for every pixel, get the color and paint or skip for empty space

second, the order of traverse is the correct for the point of view, the AND filter the children for traverse..

images from the blog:



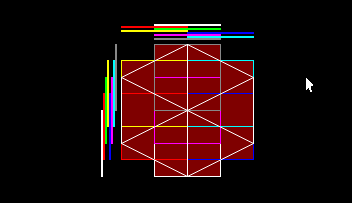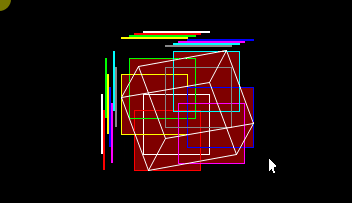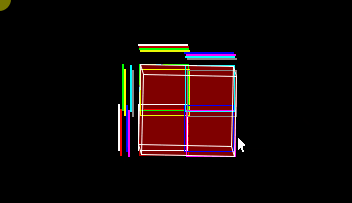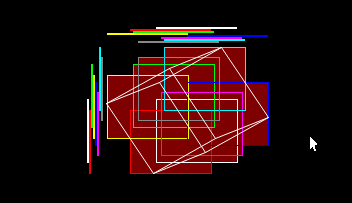
every color is a children, X array is the line up, Y array is the line left

you can see with a octree


for every pixel in X,Y
get the childrens in order from BITMASK of OCTREE AND arrayx[x] AND array[y]
deph traverse, when in, modify
X = (X - iniX )*2
Y = (Y - iniY)*2
if final node.. get te color
if no node up, restore X,Y prev
if no more nodes.. skip this pixel

at last the problem with 3d is the division operation, all is for avoid this

Reminds me of https://www.iquilezles.org/www/articles/volumesort/volumesort.htm.

The order of visit of the children is not the key here. In fact, I use the simplest version of the Quilez article.

In fact, in an isometric perspective, this order does not change when you descend on the tree, in real perspective, yes.

So it seems the idea here is to use bit operations to make the intersection tests between the rays and octree nodes simpler, right?

yes, you are rigth!