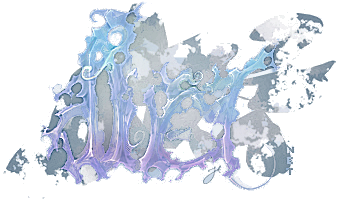
Signed distance to quadratic bezier
category: code [glöplog]
mind = blown
does this thread means that we will see some smooth raymarched boobs in asm compos next year ?
I'd be in for some raymarched scenepoetry.
what is SDF ?
T21 : how do you render your last image ? is it a pixel shader who access to all your Quadratic curves segment ?
beacuse I don't undertstand the meaning of your x += .. parameter in a pixel shader.
T21 : how do you render your last image ? is it a pixel shader who access to all your Quadratic curves segment ?
beacuse I don't undertstand the meaning of your x += .. parameter in a pixel shader.
SDF = signed distance field.
Once you have evaluated distances you can perform interesting operations. Those might become texture the GPU can render using trivial shaders.
BTW, you might have noticed that the distance function doesn't return negative value, but I do have crossing test that turn distance negative inside shapes.
The code is currently running on the CPU, making this screen based skipping possible.
On the GPU you would render in multiple pass. If you use plain pixel shaders, you would use regular grids. Possibly start at 32x32 resolution and go down to 4x4. (4 pass)
Once you have evaluated distances you can perform interesting operations. Those might become texture the GPU can render using trivial shaders.
BTW, you might have noticed that the distance function doesn't return negative value, but I do have crossing test that turn distance negative inside shapes.
The code is currently running on the CPU, making this screen based skipping possible.
On the GPU you would render in multiple pass. If you use plain pixel shaders, you would use regular grids. Possibly start at 32x32 resolution and go down to 4x4. (4 pass)
T21: ok it was my thougth. Because i have already implemented quadratic curve rendering with pixel shader with the same technic ( sdf )
Well, if you are not limited to pixel shader this could be leveraged as an early out in a compute kernel.
I haven't tried to optimize the pants off this yet, I usually let this type of code simmer for weeks before I truly go parallel.
BTW, cool UI ;)
I actually downloaded your app earlier today after seeing your post in the "work in progress" thread.
I haven't tried to optimize the pants off this yet, I usually let this type of code simmer for weeks before I truly go parallel.
BTW, cool UI ;)
I actually downloaded your app earlier today after seeing your post in the "work in progress" thread.
friggin cool work :)
I have a numerical approximation for the distance to cubic bezier splines - it's pretty straight forward to implement - just some mix instructions and a little loop - all you need is a "distance to line" segment and some subdivision approach. In case there's a common interest in that code I'm willing to share it - it's "future proof" code - as in - it's slow as f*ck - depending on the number of subdivisions.
Did anyone try yet to rewrite the here proposed distance to quadratic in GLSL/HLSL? I would like to see some copy-pasteable code - because I'm lazy.
Did anyone try yet to rewrite the here proposed distance to quadratic in GLSL/HLSL? I would like to see some copy-pasteable code - because I'm lazy.
with Quadratic rendering in a pixel shader you must be carefull with the numerical stability to handle all case of the distance computing.
Because you can have numerical rounding error or cancellation of the term "r[0] = offset + u + v;"
see this link for more infos
Because you can have numerical rounding error or cancellation of the term "r[0] = offset + u + v;"
see this link for more infos
the code can be translated super easily, and it worked just wonderfully here in GLSL (#version 330 core):
Code:
float findNearestPoint( in vec3 P0, in vec3 P1, in vec3 P2, in vec3 x )
{
float d0 = length( P0-x );
float d2 = length( P2-x );
float dis = min( d0, d2 );
vec3 a = P0 - 2.0*P1 + P2;
vec3 b = 2.0*(P1 - P0);
vec3 c = P0;
float k3 = 2.0*dot(a,a);
float k2 = 3.0*dot(a,b);
float k1 = dot(b,b) + 2.0*dot(c-x,a);
float k0 = dot(c-x,b);
float res[3];
int n = solveCubic( k3, k2, k1, k0, res );
for( int i=0; i<n; i++ )
{
float t = res[i];
if( t>=0.0 && t <=1.0 )
{
vec3 pos = (1.0-t)*(1.0-t)*P0 + 2.0*t*(1.0-t)*P1 + t*t*P2;
dis = min( dis, length( pos - x ) );
}
}
return dis;
}does this help performance?
Code:
float findNearestPoint( in vec3 P0, in vec3 P1, in vec3 P2, in vec3 x )
{
float d0 = length( P0-x );
float d2 = length( P2-x );
float dis = min( d0, d2 );
vec3 a = P0 - 2.0*P1 + P2;
vec3 b = 2.0*(P1 - P0);
vec3 c = P0;
float k3 = 2.0*dot(a,a);
float k2 = 3.0*dot(a,b);
float k1 = dot(b,b) + 2.0*dot(c-x,a);
float k0 = dot(c-x,b);
float res[3];
int n = solveCubic( k3, k2, k1, k0, res );
float t = saturate(res[0]);
vec3 pos = (1.0-t)*(1.0-t)*P0 + 2.0*t*(1.0-t)*P1 + t*t*P2;
dis = min( dis, length( pos - x ) );
if(n>1) {
t = saturate(res[1]);
pos = (1.0-t)*(1.0-t)*P0 + 2.0*t*(1.0-t)*P1 + t*t*P2;
dis = min( dis, length( pos - x ) );
t = saturate(res[2]);
pos = (1.0-t)*(1.0-t)*P0 + 2.0*t*(1.0-t)*P1 + t*t*P2;
dis = min( dis, length( pos - x ) );
}
return dis;
}
Here is a full GLSL sample of the code outlined here for reference.
Because all the math is so obvious there is no comments :)
http://glsl.heroku.com/e#4966.4
Because all the math is so obvious there is no comments :)
http://glsl.heroku.com/e#4966.4
Extending it to draw a curve of splines is a piece of cake:
http://glsl.heroku.com/e#4971.0
http://glsl.heroku.com/e#4971.0
This is totally awesome work! but oh dear lord - how long till we get endless message scrollers :P
Actually this is real progress : http://glsl.heroku.com/e#4973.0
u2: Yes, well clearly you have walked that path before.
Do you have a solution for http://glsl.heroku.com/e#4966.21
Because with
p[1] = vec2(resolution.x*.45,resolution.y*.5);
it breaks exactly for the reason the mentioned.
Tigrou, cant wait for you to complete your Pinocchio.
Do you have a solution for http://glsl.heroku.com/e#4966.21
Because with
p[1] = vec2(resolution.x*.45,resolution.y*.5);
it breaks exactly for the reason the mentioned.
Tigrou, cant wait for you to complete your Pinocchio.
@T21 : i had some difficulties to implement the mouth...
I have an alternative proof of concept of what I mentioned in my first post.
(no for(), if(), acos(), cos(), sin(), cuberoot() in this version)
But because it require the UV gradient, I dont think its any faster...
http://glsl.heroku.com/e#4976.1
For the curious
(no for(), if(), acos(), cos(), sin(), cuberoot() in this version)
But because it require the UV gradient, I dont think its any faster...
http://glsl.heroku.com/e#4976.1
For the curious
Tigrou : HAHAHAH you save my day :)
T21 : I use this trick to compute the return parameter D is positive :
sorry my variables perhaps deosn't match yours but the trick is to avoid the float cancellation when substracting little value.
Llittle more thing to say. I have traced with NSight the behavior of float operations on a GTX280 and it's not as accurate as the code generated by the CPU. If I run the same code on the CPU the resulat is less prone to float cancellation than on the GPU.
T21 : I use this trick to compute the return parameter D is positive :
Code:
if( abs(p3_27) < q2*0.001 )
{
if( q <0 )
ret = u + offset + p / ( 3.f * -pow(-q,1.f/3.f) ) ;
else
ret = v + offset + p / ( 3.f * pow(q,1.f/3.f) ) ;
}
else
{
ret = u + v + offset
}
sorry my variables perhaps deosn't match yours but the trick is to avoid the float cancellation when substracting little value.
Llittle more thing to say. I have traced with NSight the behavior of float operations on a GTX280 and it's not as accurate as the code generated by the CPU. If I run the same code on the CPU the resulat is less prone to float cancellation than on the GPU.
Thx.
Here is a third method. from
http://research.microsoft.com/en-us/um/people/hoppe/ravg.pdf
(See fig 7)
http://glsl.heroku.com/e#5007.0
Here is a third method. from
http://research.microsoft.com/en-us/um/people/hoppe/ravg.pdf
(See fig 7)
http://glsl.heroku.com/e#5007.0
Code:
vec2 get_distance_vector(vec2 b0, vec2 b1, vec2 b2)
{
float a=det(b0,b2), b=2.0*det(b1,b0), d=2.0*det(b2,b1);
float f=b*d-a*a;
vec2 d21=b2-b1, d10=b1-b0, d20=b2-b0;
vec2 gf=2.0*(b*d21+d*d10+a*d20);
gf=vec2(gf.y,-gf.x);
vec2 pp=-f*gf/dot(gf,gf);
vec2 d0p=b0-pp;
float ap=det(d0p,d20), bp=2.0*det(d10,d0p);
float t=clamp((ap+bp)/(2.0*a+b+d), 0.0,1.0);
return mix(mix(b0,b1,t),mix(b1,b2,t),t);
}
Would it be possible to utilise this (or something similar) for modelling 3d surfaces for raymarching purposes?
i have had a look in paper. when you construct a biquadratic bezier patch, and you take the squared distance to a given point from it's surface and do the derivative(s) in order to get the closest distance, seems you get a system of two equations in degrees {4,3} and {3,4}, which leads to a solution of a polynomial of degree 7. which is not analytic. so it cannot be done just with a formula as with the quadatic bezier curve.
but i'm sure there are a million approximation and/or iterative solutions.
but i'm sure there are a million approximation and/or iterative solutions.