pass-band filter
category: general [glöplog]
Anyone know of a good algorithm for a pass-band filter? I was thinking about doing a low-cutoff and then a hi-cutoff but I'm not entirely sure if this will do the trick.
Kilroy was here ...
use a regular filter like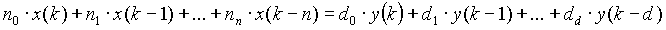 
- your output is y(k).
For fast filtering use a small amount of coefficients (N).
For N=2:
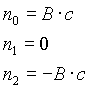
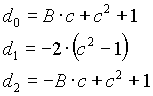
with
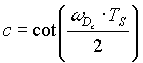
(Ts is sampling rate, ie 1/44100, Ws is the band frequency) and
B=1/Q (shape of the pass band).
Full thing is here: http://www.apicsllc.com/apics/Sr_3/Sr_3.htm and includes filters of higher order as well as low, high, and notch filters.
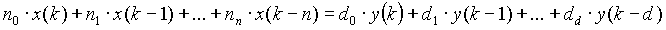- your output is y(k).For fast filtering use a small amount of coefficients (N).
For N=2:
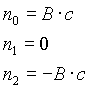
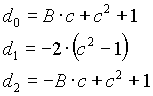
with
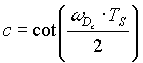
(Ts is sampling rate, ie 1/44100, Ws is the band frequency) and
B=1/Q (shape of the pass band).
Full thing is here: http://www.apicsllc.com/apics/Sr_3/Sr_3.htm and includes filters of higher order as well as low, high, and notch filters.
Thanks fella, Audio-EQ-Cookbook.txt looks promising. I'll let you know how it goes probably later on tonight
... although probably slow
Look through musicdsp.org archive - they have one really kicking passband filter there (which I'm using in almost all my 4k's).
kk> Wow, looks nice. Which one do you use?
There is no such thing as a pass-band filter.. Each filter has a pass-band (some even have two...). The Pass-Band response of a filter is the characteristic a filter has at the ... well ... pass-band. The point where the response raises or lowers...
There is no dedicated pass-band filter though. When talking about pass-band we're talking about slope, ripple, ringing within that critical part of the frequency spectrum...
I think you're looking for a BAND-pass filter.. If so check out bi-quad filters.. You can also build a simple bandpass by chaining a simple high- and low-pass filter, but you will have a rather poor pass-band response :-)
There is no dedicated pass-band filter though. When talking about pass-band we're talking about slope, ripple, ringing within that critical part of the frequency spectrum...
I think you're looking for a BAND-pass filter.. If so check out bi-quad filters.. You can also build a simple bandpass by chaining a simple high- and low-pass filter, but you will have a rather poor pass-band response :-)
Sigflup, if it's for a synth a good starting point is the state variable filter. It gives lowpass, bandpass and highpass in one structure:
hp = input - lp - bp*q;
bp = bp + f*hp;
lp = lp + f*bp;
(init: bp = 0, lp = 0, which are the filter states.)
f controls frequency: f = 0 .. 1.0
q controls 'resonance' q = 1.0 .. almost zero (watch your ears!)
It is not a perfect filter in the sense that the lowpass cutoff frequency does not go all the way to the nyquist frequency. And you don't have complete control the bandwidth of the bandpass output. But it's a simple filter and it works really well.
The filter is a 12dB/octave system. To get a better bandpass, simple concatenate two filters (one lowpass and one highpass).
As Torus said, biquads (see that Bristow-Johnson EQ document) allow more control but are a b*tch to modulate.
@Torus: there is nothing against concatenating digital filters.
hp = input - lp - bp*q;
bp = bp + f*hp;
lp = lp + f*bp;
(init: bp = 0, lp = 0, which are the filter states.)
f controls frequency: f = 0 .. 1.0
q controls 'resonance' q = 1.0 .. almost zero (watch your ears!)
It is not a perfect filter in the sense that the lowpass cutoff frequency does not go all the way to the nyquist frequency. And you don't have complete control the bandwidth of the bandpass output. But it's a simple filter and it works really well.
The filter is a 12dB/octave system. To get a better bandpass, simple concatenate two filters (one lowpass and one highpass).
As Torus said, biquads (see that Bristow-Johnson EQ document) allow more control but are a b*tch to modulate.
@Torus: there is nothing against concatenating digital filters.
sigflup: If I remember correctly I was using the one labelled "Peak/Notch Filter" (although I've dropped notch functionality completely).
trc_wm: It's the perfect filter in the sense of space usage in 4k intro. ;) Pretty lightweight with practically no need for coeff computation.
As for "to get better bandpass use hi- and low-pass" part, that's not exactly true. This way you'll still get 12dB/oct slopes. To get better bandpass, stack together two exactly the same bandpass SVF filters. The same holds for most other filter types*, especially if you want a nice 24dB/oct lowpass for your bass.
*) Stacking these peak/notch filters from musicdsp.org won't do much good, as single one is already capable of really steep slopes.
trc_wm: It's the perfect filter in the sense of space usage in 4k intro. ;) Pretty lightweight with practically no need for coeff computation.
As for "to get better bandpass use hi- and low-pass" part, that's not exactly true. This way you'll still get 12dB/oct slopes. To get better bandpass, stack together two exactly the same bandpass SVF filters. The same holds for most other filter types*, especially if you want a nice 24dB/oct lowpass for your bass.
*) Stacking these peak/notch filters from musicdsp.org won't do much good, as single one is already capable of really steep slopes.
Quote:
As for "to get better bandpass use hi- and low-pass" part, that's not exactly true. To get better bandpass, stack together two exactly the same bandpass SVF filters.
Sorry, my original statement wasn't clearly enough:
To get a bandpass with controllable bandwidth, concatenate a lowpass and highpass.
Or use Q accordingly.
no.
Use Q?
Q uses you!
Q uses you!
@trc_wm: yes.
http://www.rane.com/pdf/ranenotes/Bandwidth%20in%20Octaves%20vs%20Q%20in%20Bandpass%20Filters.pdf
http://www.rane.com/pdf/ranenotes/Bandwidth%20in%20Octaves%20vs%20Q%20in%20Bandpass%20Filters.pdf
Those filters (like the state variable "bandpass" filter above) are not true bandpass filters. They're resonators as they don't have a nice flat passband, like this.
In addition, the 'q' parameter of the state variable filter also varies its gain. This property is a feature of resonators.
I agree that you can change the bandwidth of a resonator; I just don't think of them as bandpass filters.
In addition, the 'q' parameter of the state variable filter also varies its gain. This property is a feature of resonators.
I agree that you can change the bandwidth of a resonator; I just don't think of them as bandpass filters.
trc_wm: OK, this way you'll be able to control flat region of the bandpass filter, but it wtill won't be very steep (12 dB/oct on each side).
As for using Q (the filter one, not this guy) - it's completely doable, you just have to get a filter which has correctly implemented Q parameter (check that peak/notch filter I've mentioned - it has perfect Q behavior).
And when it comes to q parameter of SVF - why don't compute gain at middle frequency analytically as a function of q and elliminate the gain boost.
As for using Q (the filter one, not this guy) - it's completely doable, you just have to get a filter which has correctly implemented Q parameter (check that peak/notch filter I've mentioned - it has perfect Q behavior).
And when it comes to q parameter of SVF - why don't compute gain at middle frequency analytically as a function of q and elliminate the gain boost.
As a proof of concept of what KK said, here is a bandpass biquad with a flat magnitude response. There is no conceptual difference between resonators and bandpass.
(with Todybear Filter Explorer).
(with Todybear Filter Explorer).
c0 controlling the cutoff and c1 the bandwidth
Quote:
As a proof of concept of what KK said, here is a bandpass biquad with a flat magnitude response. There is no conceptual difference between resonators and bandpass.
The difference is that a resonator does not have any zeros.
Your biquad example has two zeros and is therefore not a resonator but a 'true' bandpass filter which, as I wrote earlier, can have an (almost) flat passband.
However, your example says nothing because the screenshot does not show any numbers along the axes or if the responses are on a linear or logarithmic scale. You can make anything look flat by zooming out.
OK, you are right and i'm talking shit about resonators.
(btw the magnitude response plot goes to 0 to nyquist)
I'm confused because i can't imagine a filter without a zero...
(btw the magnitude response plot goes to 0 to nyquist)
I'm confused because i can't imagine a filter without a zero...
