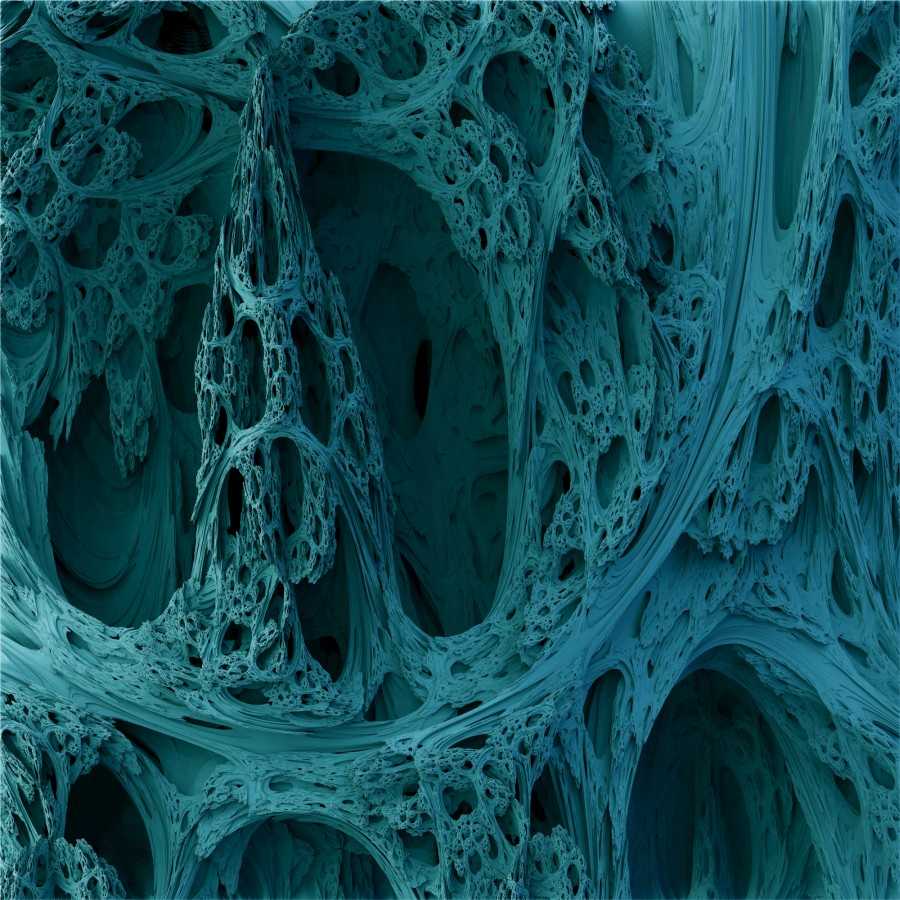
Astonishing 3D mandelbrot renderings
category: general [glöplog]
Quote:
kurli, it isn't 1989 anymore you know :)
By that you are implying that rendering these would be possible today? Bruteforce? I'm waiting :)
picture of a Sea urchin fractal, a natural one that is:


very nice site :)
uuh. are those titties? !takki
I think you can enter your formula's into something like http://www.chaoscope.org/ and get "3D" render's too.
cool stuff :) made me do my own mandelbulb renderer:

nothing special atm but it's a start

nothing special atm but it's a start
looking good src
I need to optimize the formula before I even start implementing my own renderer. All those conversions from cartesian to polar and back are so redundant.
Still, I really want to navigate inside those openings and see what kind of mysteries lie inside!
Still, I really want to navigate inside those openings and see what kind of mysteries lie inside!
viznut, you can practice by optimizing trigonometry away from, say, taking a cube root of a complex number.
Vinzut, for "z -> z^8 + c" you can use
It's one inverse square root per iteration. Speed gain over the trigonometric function is a 4x or 5x for the CPU version. I didn't see much gain (if any) in the GPU version.
Trigonometric version:
(where here z is the (x,y,z) triplet of the polynomial version.
Code:
float x2 = x*x; float x4 = x2*x2;
float y2 = y*y; float y4 = y2*y2;
float z2 = z*z; float z4 = z2*z2;
float k3 = (x2+z2);
float k2 = inversesqrt( k3*k3*k3*k3*k3*k3*k3 );
float k1 = x4 + y4 + z4 - 6.0*y2*z2 - 6.0*x2*y2 + 2.0*z2*x2;
x = a + 64.0*x*y*z*(x2-z2)*(x2-y2+z2)*(x4-6.0*x2*z2+z4)*k1*k2;
y = b + -16.0*y2*(x2+z2)*(x2-y2+z2)*(x2-y2+z2) + k1*k1;
z = c + -8.0*y*(x2-y2+z2)*(x4*x4 - 28.0*x4*x2*z2 + 70.0*x4*z4 - 28.0*x2*z2*z4 + z4*z4)*k1*k2;
It's one inverse square root per iteration. Speed gain over the trigonometric function is a 4x or 5x for the CPU version. I didn't see much gain (if any) in the GPU version.
Trigonometric version:
Code:
float zr = sqrt( dot(z,z) );
float zo = acos( z.y/zr );
float zi = atan( z.x, z.z );
zr = pow( zr, 8.0 );
zo = zo * 8.0;
zi = zi * 8.0;
z = vec3(a,b,c) + zr*vec3( sin(zo)*sin(zi), cos(zo), sin(zo)*cos(zi) );
(where here z is the (x,y,z) triplet of the polynomial version.
iq: how do you calculate your normals? this is my normal generating code atm:
it's just some trial and error code i threw together that produced results that weren't to shabby but i feel that there is a lot of room for improvements.
current result:

Code:
private Vector getNormal(Vector pos) {
double xG = 0.0;
for(double i = 0; i < 5; i += 1.0)
xG += (nbIterations(8.0, new Vector(pos.x - e * i, pos.y, pos.z)) - nbIterations(8.0, new Vector(pos.x + e * i, pos.y, pos.z))) / (i + 1.0);
double yG = 0.0;
for(double i = 0; i < 5; i += 1.0)
yG += (nbIterations(8.0, new Vector(pos.x, pos.y - e * i, pos.z)) - nbIterations(8.0, new Vector(pos.x, pos.y + e * i, pos.z))) / (i + 1.0);
double zG = 0.0;
for(double i = 0; i < 5; i += 1.0)
zG += (nbIterations(8.0, new Vector(pos.x, pos.y, pos.z - e * i)) - nbIterations(8.0, new Vector(pos.x, pos.y, pos.z + e * i))) / (i + 1.0);
return (new Vector(xG, yG, zG)).norm();
}
it's just some trial and error code i threw together that produced results that weren't to shabby but i feel that there is a lot of room for improvements.
current result:


I added the distance estimation to the marcher, so now it´s officially a distance field raymarcher as in the "old" days.

Close up.

I plan to add analytical distance computation so it should be realtime very soon - it takes a couple of seconds to render right now.
src, I´m using a 4 point central difference to approximate the gradient. That you be enough provided your nbIterations() return a float instead of an int. Are you using the smooth-iteration-counter? Something like this?
nbIterations = n + 1 - log(log(|Z|)/log(2)
If you are not, try it in 2D in a regular M-Set to make sure you get it working there first... You want to get a smooth color gradient image instead of the classic banded escape time image.

Close up.

I plan to add analytical distance computation so it should be realtime very soon - it takes a couple of seconds to render right now.
src, I´m using a 4 point central difference to approximate the gradient. That you be enough provided your nbIterations() return a float instead of an int. Are you using the smooth-iteration-counter? Something like this?
nbIterations = n + 1 - log(log(|Z|)/log(2)
If you are not, try it in 2D in a regular M-Set to make sure you get it working there first... You want to get a smooth color gradient image instead of the classic banded escape time image.
el-bee: which demo is that screen from?
ezmic: http://www.pouet.net/prod.php?which=25777 (one of my favourite 64ks.. i don't think there's any fractals in it, but it's full of beautiful maths. And design and music. :)
iq: I'd be interested to see how it animates with these approximated gradients (given that there's no actual gradient to approximate on a fractal surface). Any way you could easily render an animation of it?
IQ: are you planning to make it interactive so it can be explored? I'm wondering how the hell you control motion around something like this.. guess you'd need movement + rotation to move around it, then a zoom control that also scales the movement so you can zoom in and move around the small structures?
Good work on there - I'm looking forwards to seeing that as a demo or something :)
Good work on there - I'm looking forwards to seeing that as a demo or something :)
wow looking forward to this one, assuming it will become a scene release.
With spacenavigator or some other 6-dof controller?
..of course you need to hack zooming in somehow on top of those, but something like click+forward would probably work well enough
..of course you need to hack zooming in somehow on top of those, but something like click+forward would probably work well enough
216: mouse to rotate, click for forwards was what I thought too, but it doesn't really work. If you move forwards at constant speed (needs to be reasonably fast to get all the way round the object), you can look around the whole object easy enough, but for a fractal you also want to study small areas for the detail.. then smaller still areas, then...
Thinking about it a bit more, I think a combination of mouse movement + trackball (the software type) + exponential zoom could work well. Move the mouse around to "walk" around the object, hold down button + move it to rotate the object about a point in front of the camera, then maybe hold right-button and move to zoom in/out. Zoom would have to be exponential, otherwise it ends up too slow at first then too fast when you're zoomed right in.
If iq releases some shader source I'll plug it into quartz composer and set up and interactive version. That would be osx only though.
Thinking about it a bit more, I think a combination of mouse movement + trackball (the software type) + exponential zoom could work well. Move the mouse around to "walk" around the object, hold down button + move it to rotate the object about a point in front of the camera, then maybe hold right-button and move to zoom in/out. Zoom would have to be exponential, otherwise it ends up too slow at first then too fast when you're zoomed right in.
If iq releases some shader source I'll plug it into quartz composer and set up and interactive version. That would be osx only though.
iq: thx for the hint with the smooth iteration counter, seems to work fine (i'll post images later) :)
are you taking the "Exterior distance estimation" for the distance field described on Wikipedia or something else? i would be very interested in a distance field because you don't have to do the iteration thing at all if you have a good distance field -> faster and less branches -> realtime on gpu :D
are you taking the "Exterior distance estimation" for the distance field described on Wikipedia or something else? i would be very interested in a distance field because you don't have to do the iteration thing at all if you have a good distance field -> faster and less branches -> realtime on gpu :D
doom, there is no problem with animations, as what you see here it not a true mathematically correct fractal, but just an approximation with a limited amount of iterations. The surface you get when truncating the amount of iterations is a harmless polynomial surface with perfectly defined normal, so no problem at all. Think kindernoiser Another way to see is like this: with one iteration you get a disk(2D)/sphere(3D) approximation to the M-Set, that's a 2 degree poly. With 2, some sort of egg shaped thing (degree 4). With three iterations it's some funky distorted egg (deg 8), etc. After say 10 iterations you get a complex polynomial shape, but still perfectly smooth with derivatives and all the stuff. We never render real fractals, only things that are more or less close to it.
iq: I know it's not mathematically a fractal. :) But what I mean is, if you want to be able to zoom in and reveal "a lot" of detail you'd want a "high" max iteration count. So those 4 samples would have to be close enough together to reflect the actual complexity of the surface as it's approximated, but that means when you're not zoomed in all you get is noise for the complex regions.
psionice: Exponential zoom is good, but you need to apply it to rotation as well, otherwise if you're zoomed in on some detail it'll vanish as soon as you rotate just a little bit.
Probably better to have a 6-DOF camera which can rotate freely and move along the view direction, but with movement that slows down exponentially as the camera gets "closer" to the surface. I'm thinking the escape time of a single point at the camera's position might be a good (and readily available) distance measure for that purpose.
Or not.
psionice: Exponential zoom is good, but you need to apply it to rotation as well, otherwise if you're zoomed in on some detail it'll vanish as soon as you rotate just a little bit.
Probably better to have a 6-DOF camera which can rotate freely and move along the view direction, but with movement that slows down exponentially as the camera gets "closer" to the surface. I'm thinking the escape time of a single point at the camera's position might be a good (and readily available) distance measure for that purpose.
Or not.
doom: yeah, true. Movement speed would scale with zoom, that's easy enough, but rotation could be tricky. Trackball systems rotate around a sphere, with the centre of the sphere x units from the camera, so you'd definitely want x to scale with the zoom. But you'd ideally want x = distance from surface in the centre of the screen, so you always rotate about the surface. I guess that can be calculated on the CPU. You wouldn't want to actually take the current distance from the screen, because when you rotate the distance changes and you'd have jitter hell..
I'm looking forwards to trying this :) (In a 32x32 window most likely as my GPU is neither new or high end...)
I'm looking forwards to trying this :) (In a 32x32 window most likely as my GPU is neither new or high end...)