Random image thread
category: residue [glöplog]
damnit people:p
to calculate impossible values we use limits
and what's lim(x->0) of a/x ?
exactly -infinity and +infinity
to calculate impossible values we use limits
and what's lim(x->0) of a/x ?
exactly -infinity and +infinity
indeed, AND
both at the same time
but:

both at the same time
but:




Division by zero? Easy...
Just introduce a new number as Dr James Anderson did. Solved!
Proof:


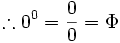
well... Not so random, so here goes:

Just introduce a new number as Dr James Anderson did. Solved!
Proof:


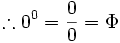
well... Not so random, so here goes:

Quote:
both at the same time
No, however you defiine division, a/0 must equal a/0. That means, if you allow a/0 = infinity, AND a/0 = -infinity, then infinity = -infinity. And then nothing makes sense anymore. E.g. infinity > x and -infinity < x for any x, so x < x.
Related to that is the result that the limit of a/x as x approaches zero doesn't exist, unless a=0, in which case the limit is 0. There are limits from above and below, but since they're not equal, there isn't "a limit", because that too would imply that infinity = -infinity.
In practical applications though, you usually want floating point convenitions along these lines:
a/0 = sgn(a) * infinity, a != 0
0/0 = NaN
infinity/infinity = NaN
NaN != NaN
So birds.
stop the talk and post a random image



oh, and: lol@LiraNuna
Quote:
Haven't seen that one since I was a kid.. it was included in a book full of caricatures and satirical cartoons that my dad had.


Nvidia GeForceFX Graphics Demo

New Nvidia Graphics Demo?


New Nvidia Graphics Demo?

Quote:
Related to that is the result that the limit of a/x as x approaches zero doesn't exist, unless a=0, in which case the limit is 0. There are limits from above and below
Actually, if lim_x->a f(x)=inf, (even if it's just a left or right handed limit) then the limit is not considered to exist. The statement "lim_x->a f(x)=inf" specifies the way in which the limit does not exist. This is pretty important for other theorems which depend on the fact that a limit "exists".
As for division by zero, you can pretty much get any result with limits depending on how you specify the dividend. For example, lim_x->0 (4x/x) = 4.

since when is this random math talk? stfu and post random image! like this:





Thanks imageshack.




